백준 12100번 2048 (Easy) : https://www.acmicpc.net/problem/12100
12100번: 2048 (Easy)
첫째 줄에 보드의 크기 N (1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 게임판의 초기 상태가 주어진다. 0은 빈 칸을 나타내며, 이외의 값은 모두 블록을 나타낸다. 블록에 쓰여 있는 수는 2보다 크거나 같고, 1024보다 작거나 같은 2의 제곱꼴이다. 블록은 적어도 하나 주어진다.
www.acmicpc.net
설명
2048은 블록을 움직이면서 같은 블록들끼리 합치면서 최대한 큰 수를 만들어 내는 게임이다.
실제 게임에서는 이동을 한 번 할 때마다 블록이 추가되지만, 이 문제에서 블록이 추가되는 경우는 없다.
이동은 상하좌우 네 방향으로만 이동할 수 있으며 같은 값을 갖는 두 블록이 충돌하면 두 블록은 하나로 합쳐진다.
문제를 풀기 전에 시간 복잡도를 계산해 보았다.
문제의 조건은 최대 5번 이동시켜 얻을 수 있는 가장 큰 블록을 얻는 것이다.
한 번 이동할 때 가능한 경우의 수는 4번이다. (상하좌우)
따라서 5번 동안 이동할 수 있는 경우의 수는 4 x 4 x 4 x 4 x 4 = 1024이다.
구현은 보드판을 2중 for문으로 탐색하면서 Stack을 사용하며 블록을 합칠 것이다.
n이 최대 20이므로 한 번 이동할 때 생기는 연산의 수는 20 x 20 = 400이다.
따라서 총 연산의 수는 1024 x 400 ≒ 400,000이다.
시간제한이 1초이므로 위의 아이디어로 충분히 풀 수 있다는 결론이 나온다. (물론 잡다한 연산은 모두 제외했다.)
시간제한이 1초면 1억 번의 연산 횟수로 생각하면 된다.
구현에는 최대값 max, 게임판 board, 블록을 쌓는 stack, 상태 체크 flag 등이 사용됐다.
max는 전역변수로 선언하여 합칠 때마다 max와 비교하며 값을 업데이트해줬다.
블록을 이동하는 것은 상하좌우 네 가지 경우가 있으므로 up, down, right, left 4개의 메소드로 분리하여 사용했다.
각각의 메소드에서는 board의 하나의 row 혹은 column을 기준으로 stack에 값을 넣었다.
stack에 넣을 때는 top의 값과 비교하여 값이 같으면 pop()을 한 뒤 새로운 값과 합하여 넣었다.
문제를 풀며 한 가지 체크해야 할 점이 있는데,

위와 같은 게임판이 있고, 왼쪽으로 이동한다고 하면 정상적이라면 아래와 같은 모습이 나와야 한다.
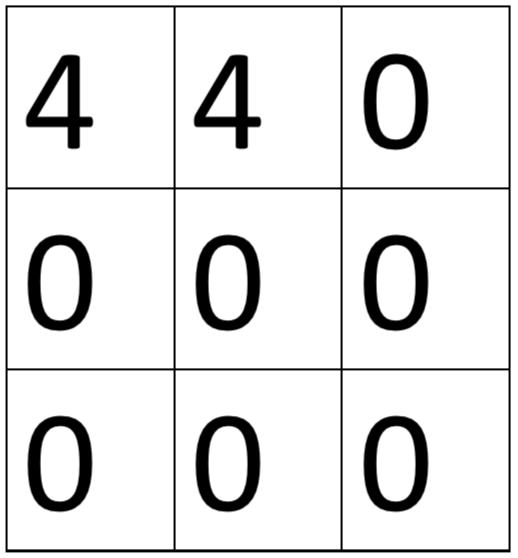
하지만 구현 결과는 아래처럼 나왔다.
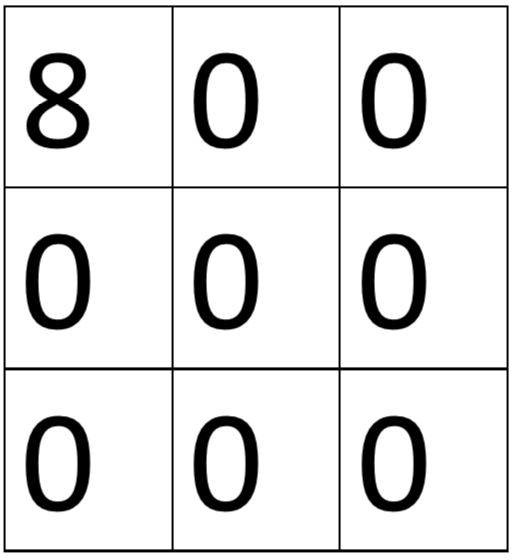
스택에 값이 쌓일 때 연속으로 2번 합치는 경우에 생기는 문제이다.
이와 같은 문제를 해결하기 위해 flag 변수를 사용했다.
디폴트 값으로는 true를 가지면서 블록이 합쳐지는 경우에만 false로 변경한다.
그 이후 그 다음 블록의 연산이 끝나면 다시 true로 변경한다.
이런 식으로 구현하면 연속으로 2번 합쳐지는 경우를 막을 수 있다.
4가지의 메소드가 구현 방식이 비슷해서 중복된 코드가 많다.
리팩토링해서 코드 수를 줄여보고자 했으나 continue와 flag를 어떤 식으로 관리해야 할지 모르겠어서 그냥 놔두었다.
코드
import java.util.Scanner;
import java.util.Stack;
public class Main {
private static int n;
private static int max;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
max = 0;
int[][] board = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
board[i][j] = sc.nextInt();
if (board[i][j] > max) max = board[i][j];
}
}
solution(board, 0);
System.out.println(max);
}
private static void solution(int[][] board, int count) {
if (count == 5) return;
solution(up(board), count + 1);
solution(down(board), count + 1);
solution(right(board), count + 1);
solution(left(board), count + 1);
}
private static int[][] up(int[][] board) {
int[][] result = new int[n][n];
Stack<Integer> stack = new Stack<>();
boolean flag = true;
for (int j = 0; j < n; j++) { // 가로로 움직이기
for (int i = 0; i < n; i++) { // 세로로 움직이기
if (board[i][j] != 0) {
if (stack.size() == 0) stack.add(board[i][j]);
else {
if (stack.peek() == board[i][j] && flag) { // 블록 합치기
stack.add(stack.pop() + board[i][j]);
flag = false;
if (stack.peek() > max) max = stack.peek();
continue;
} else stack.add(board[i][j]);
}
flag = true;
}
}
while (!stack.isEmpty()) {
int i = stack.size() - 1;
result[i][j] = stack.pop();
}
stack.clear();
}
return result;
}
private static int[][] down(int[][] board) {
int[][] result = new int[n][n];
Stack<Integer> stack = new Stack<>();
boolean flag = true;
for (int j = 0; j < n; j++) {
for (int i = n - 1; i >= 0; i--) {
if (board[i][j] != 0) {
if (stack.size() == 0) stack.add(board[i][j]);
else {
if (stack.peek() == board[i][j] && flag) {
stack.add(stack.pop() + board[i][j]);
flag = false;
if (stack.peek() > max) max = stack.peek();
continue;
} else stack.add(board[i][j]);
}
flag = true;
}
}
while (!stack.isEmpty()) {
int i = n - stack.size();
result[i][j] = stack.pop();
}
stack.clear();
}
return result;
}
private static int[][] left(int[][] board) {
int[][] result = new int[n][n];
Stack<Integer> stack = new Stack<>();
boolean flag = true;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] != 0) {
if (stack.size() == 0) stack.add(board[i][j]);
else {
if (stack.peek() == board[i][j] && flag) {
stack.add(stack.pop() + board[i][j]);
flag = false;
if (stack.peek() > max) max = stack.peek();
continue;
} else stack.add(board[i][j]);
}
flag = true;
}
}
while (!stack.isEmpty()) {
int j = stack.size() - 1;
result[i][j] = stack.pop();
}
stack.clear();
}
return result;
}
private static int[][] right(int[][] board) {
int[][] result = new int[n][n];
Stack<Integer> stack = new Stack<>();
boolean flag = true;
for (int i = 0; i < n; i++) {
for (int j = n - 1; j >= 0; j--) {
if (board[i][j] != 0) {
if (stack.size() == 0) stack.add(board[i][j]);
else {
if (stack.peek() == board[i][j] && flag) {
stack.add(stack.pop() + board[i][j]);
flag = false;
if (stack.peek() > max) max = stack.peek();
continue;
} else stack.add(board[i][j]);
}
flag = true;
}
}
while (!stack.isEmpty()) {
int j = n - stack.size();
result[i][j] = stack.pop();
}
stack.clear();
}
return result;
}
}'Algorithm > Baekjoon Online Judge' 카테고리의 다른 글
| [백준] 1062번 가르침 (Java) (4) | 2020.02.12 |
|---|---|
| [백준] 15683번 감시 (Java) (0) | 2020.02.12 |
| [백준] 5397번 키로거 (Java) (0) | 2020.02.06 |
| [백준] 3190번 뱀 (Java) (2) | 2020.02.02 |
| [백준] 17779번 게리맨더링2 (Java) (0) | 2020.01.07 |
